




Several years ago I was troubled by my inability to relate the law of three to the law of seven. In particular I wanted to see how they related in the enneagram, how the triangle and web figure interacted. It was bothering me one day to the extent that I felt a need to go take a walk and think about it, hoping some insight might come from that sort of concentration on the subject. To save you any suspense, no such insight occurred, and the walk would be long forgotten were it not for an incident that I've long remembered.
In a way I cannot describe but that had proved profoundly fruitful some years before, I attempted to "follow my muse" and eventually arrived at a favorite spot near a pine on some cliffs overlooking the Pacific. Somewhat distracted, I noticed an old matchbook lying on the ground and picked it up out of some idle curiosity or other. It had printing in an oriental language on it which I could not read, but it also had a symbol or perhaps the emblem of some company on it, which looked something like this:

And beneath the symbol, in the only English anywhere on it were these words:
Link Triad Brand
I found it curious enough to pocket, but thought little about it at the time. I emptied the contents of my pockets on a table in the hall of my home, and when I later walked through the hall my eyes were attracted by some effect of the sunshine that displayed a rainbow across the matchbook lying on the table. I must have been in a superstitious mood that day, because I recall writing down which colors fell on which parts of the symbol. I may still have those notes somewhere, but my point now is that the symbol stuck and, over the next few months, I began to think more about it.

When next I gave it my full attention, it developed quickly. First, I straightened out the triangles, so that just the angles touched. Now it looked like this:
Then, seeing that the triangles formed one large equilateral triangle, I put a circle around it to form the enneagram symbol without the inner-web but with the inner triangles:

And, later, I put circles around the three "upright" triangles as well:

This, then, is the "symbol" I want to write about here.

One of the first things I tried is to put colors on the symbol. The most obvious approach seemed to be to make the whole circle white light and then assign red, green, and blue to the three smaller circles (three primary colors that can be combined in light to create all others), and this is what I got:
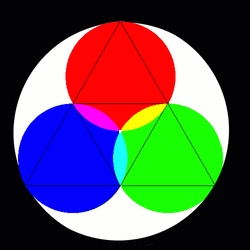
One noticeable feature is the way that white light, broken into the three primary colors, produces three more colors where the primaries overlap. Less noticeable but also observable is that the overlap of the three secondary colors then produces white light once again at the very center of the image. This is something that is often forgotten in the prism experiments of Isaac Newton: White light not only breaks down into colors, but the colors recombine to produce white light. More immediately for me, what I saw was a way that the law of three relates to the law of seven, just what I had set out to find originally: The three colors produced three others, making six. And these six colors originated from, and recombined into, the seventh, white light. In this diagram, white light is "Do"—the alpha and omega of an octave, the octave of visible light. [1]

I was reading about "sacred geometry" recently, and noticed that this:

Another way to view this symbol is in terms of the ancient "Four Elements":
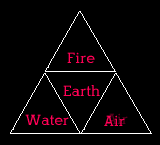
I bought a book for very little in a catalog sale to see what I could find out about the cover art, that looked like this:
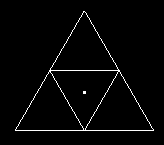
Note the point in the middle. This again expresses the seventh. (The book, incidentally, was The Hymns of Hermes, written by G. R. S. Mead, who clearly had a profound understanding of Gnostic/Hermetic ideas.)
But now I find this as a "frontispiece" of a book by Jacob Boehm, the German religious mystic of the 16th-17th centuries:
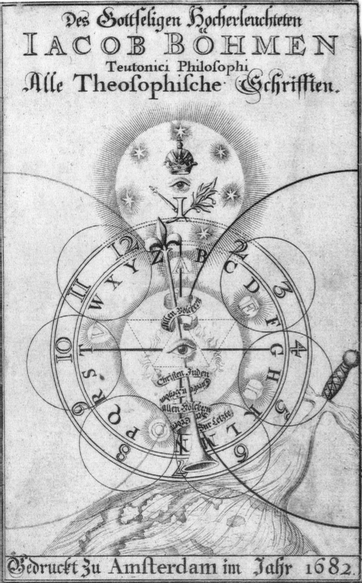
While considerably more elaborate, this includes the triangle with the reverse included in the center, but inverted. Seven explicitly with the seven circles.

One of the more interesting things about this symbol is that it may repeat, that is, what we have shown so far is just the first iteration of it. The inner, upside-down triangle contains within it a right-side-up triangle, and the sequence continues for the duration of whatever is being discussed. When viewed as the Ray of Creation for example, many "inner" triangles are involved as the representation proceeds further down the Ray. The symbol below, for example, represents world 48:

We can view this symbol from "above" or "below", so to speak. Viewed from above, we see how insignificant world 48 appears from world 3. Or, viewed from below, we see how distant world 3 appears from world 48. The latter, for example, gives a visual representation of the small part the laws of world 3 play in world 48.

The triangles in the symbol are similar to the old Star of David or Solomon's Seal:

I was surprised to see the circles all over Europe. This is the trefoil of Gothic architecture (shown above the doorways in the following image):


Then there are what are called "Borromean Rings". Three rings that link together in such a way that no individual circle links only with any other. http://www.liv.ac.uk/~spmr02/rings/trinity.html.) Removing any one ring disconnects the others:
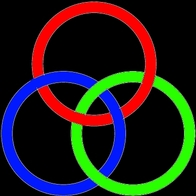
If instead of three rings we were to take a single string and make three loops, we would have what is called a torus knot. This is called the 2-3 torus knot, the simplest of the torus knots, and is also known as the trefoil knot.
The trefoil knot loops through the center of the torus three times, and the torus itself requires seven colors for mapping (http://www.hypersphere.com/hs/abouths.html#fn). So here again we seem to see the three/seven relationship.

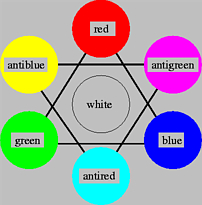
I prefer mine:


Notes

All pages Copyright © John Raithel